The Cerebellar Model Articulation Controller (CMAC), a neural network based on the concept of sensory encoding using local receptive fields, was introduced by Albus[Albus 75]. A close parallelism has been discovered between the representation of a function by a Generalized CMAC(GCMAC) and Nyquist sampling theory[González 97], discussing the role of different parameters and components of the network according to this similarity. Based on this, this paper presents a way to design automatically the CMAC architecture.
The output of the CMAC can be expressed as
Based on the above expression, it is possible to distinguish three important characteristics in the approximation of a function by a GCMAC neural network. The approximation is only possible to be done in a limited interval defined by q(x), there is a sampling processes given by the sampling function ws(x), and an interpolation function given by fg(x) to obtain a desired function. The Fourier Transforms of a function approximated by a GCMAC is given by the equation
From this equation, it is possible to have a better criterion in order to calculate the optimum parameters. The weighting sampled function spectrum Ws(W) is a set of replicas of function W(W). The bandwidth of the basis function spectrum Fg(W) has to be determined by the generalization vector in order to obtain a low frequency GCMAC output. The function Q(W) sometimes called the windowing function determines the "frequency resolution" of the GCMAC output.
The original CMAC architecture has hyper-cubic arrangements for the receptive fields, a displacement vector equal to one in all the dimensions, generalization parameter (the number of overlays) equal to r max, and binary receptive field sensitivity functions. The method presented in this paper to design automatically the GCMAC architectures is based on the possibility of selecting appropriate functions and parameters to approximate a given function by considering its spectral characteristic. It is based on the following three steps:
1. Characterizing the function from its samples can be done in two different ways; the first one is to establish a large CMAC, which the weights vector is, at most, the same size as the number of samples (it means to have a small generalization vector ) with it guarantees that the function will not be distorted because small values of generalization vector produces a large separation between the replicas. The second one consists in using a direct estimation spectral analysis.
2. Calculating the optimum generalization vector it is possible to calculate the generalization vector considering the relationship established between the generalization vector and sampling frequency. The generalization vector has to be increase in all the dimensions which correlation function among neighbor weights are above of a certain threshold level. With this information it is possible to find the spectrum replications caused by the sampling process that have to be eliminated. It only has to be considered that the basis function in the frequency domain must not have zeroes in the band of interest, and aliasing has to be avoided among the spectrum replications.
3. Calculating the displacement vector it must be selected in such a way that minimum distance between replicas is maximized in order to eliminate all the replicas that interfere with the desired signal.
Calculating the optimum displacement vector is necessary to take a closer look at the weighting sampled function. The weighting sampled function spectrum is a set of replicas of functions W(W). The separation between these replicas is primarily determined by generalization vector.
The frequency location of the replicas is given by
So(W) is the so(x) Fourier Transform. It is a train of impulses where each impulse is located in each receptive field. B(W) can be rewritten as
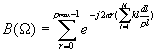
Based on the above expression, it is possible to choose the weight spectrum replications that are to be eliminated in order to calculate displacement vector. It is possible because for some values of kl , B(W) takes a value equal to zero. It means that the replica located at frequency kl is suppressed (because of the sinusoidal orthogonality property). It will permit the elimination of the spectrum replications that are not needed and the calculation of the displacement vector.
The expression in the parentheses allows one to find the displacement vector. Solving the expression in parentheses, a Genetic Algorithm is used. Genetic Algorithms have been used to solve difficult problems with objective functions that do not posses "nice" properties [Goldberg 89]. These algorithms maintain and manipulate a family, or population of solutions and implement a "survival of the fittest" strategy in their search for better solutions. The chromosome or individual used in this work is made up of a sequence of genes, where the alphabet consists of integer numbers. The first N elements represent the displacement vector and the other 2M elements represent M numbers (M equations), which is any integer other than any multiple of rmax.
The detailed description of the method, as well as selected examples will be presented at the full paper.
References
[Albus 75] J. Albus, A new approach to Manipulator Control: the Cerebellar Model Articulation Controller. Journal on Dynamic System, Measurements and Control, vol. 63, núm 3, págs 220-227, sep. 1975.
[Goldberg 89] D. E. Goldberg. Genetic Algorithms in search, optimization and machine learning. Addison-Wesley Publishing Company, 1989.
[González 97] F.J. González Serrano, A. Artés Rodríguez, A. R. Figueiras Vidal. Fourier Analysis of the Generalized CMAC neural network. It has been accepted for Publication in Neural Networks.