Keywords: Bayesian Inference, Expectaction Maximization (EM) Algorithm, Conjugate Densities, Mixture Models, Image Segmentation, Smooth Tracking.
Probabilistic modeling is a useful methodology to solve many real world data processing applications. In many of these applications a model of the data must be obtained and continuously actualized from on-line changes in the input data. In such fields, it is possible to adapt some probabilistic learning techniques in order to obtain simple, though operative and fast algorithms. The speed requirement is clearly justified when the input is continuously updated and real time response is needed. Computer vision is one of these fields, in which the frame images must be quickly processed as they change in time.
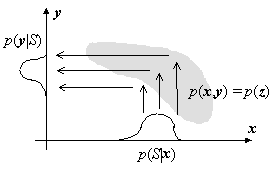
Generic probabilistic inference can be roughly outlined in Figure 1. It shows how we can use a priori knowledge of the domain - relations between the variables of interest, in the form of a joint distribution - in order to obtain a prediction for any of the output (unknown) y variables when we feed the system with some kind of information S on the input variables x.

This kind of generic inference requires a great computational effort if we do not impose some conditions in the functions involved. If we have an original joint density p(z), and the information S on the input variables x (a sub-vector of z) is given in a general likelihood form p(S|x), then the problem of estimating the posterior density p(z|S) - in order to obtain p(y|S) by marginalization (being y the sub-vector of the output variables, not necessarily disjoint of x; both of them could even be the same), can be very expensive in numerical computation:
However, if we impose some regularity conditions in the densities involved, many computations can be made analytically, and the model keeps useful even in situations where speed is critical. For example, when the joint density of the domain and the likelihood of the input variables are approximated by mixtures of factorized normals, the above formula can be significantly reduced by taking advantage of the conjugate properties of this distribution. If the domain and the likelihood are modeled respectively by
(where p r, h r and e r depend explicitly on the observed so), then the posterior can be also written as the following mixture:
where the parameters n i,r , l i,r and the weights q i,r are given by:
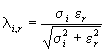
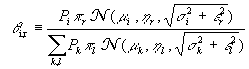
Both tasks of inference and learning can be efficiently computed with these assumptions, and therefore used in on-line applications. We summarize, in the rest of this extended abstract, how do we use these tools, as well as related ones, to perform several computer vision tasks.
Real Time Tracking of Objects
The conjugate properties of gaussian densities lead to a simple and efficient method for estimation of dynamically changing magnitudes from noisy measurements. This can be illustrated in the problem of smooth tracking of objects using a mobile camera located on a pan-tilt unit. The available measurement eo is the observed center of the object (each coordinate is treated independently), which is computed from an estimation of the contour obtained after a thresholding stage based on the ideas presented below. From the observations eo(t) taken in successive image frames, we must estimate the true velocity and position of the object, in order to set the appropriate velocity command to maintain the object centered in the camera. Note that the observed velocity:
Dynamic Thresholding for Multilevel Region Segmentation
Another interesting application of on-line inference tools is image segmentation. More specifically, we used the EM algorithm to find "separable" components in an image histogram, which is the empirical approximation to the density function of the light intensity in the image. If we have different gray level ranges in the objects of an image, we could try to model its histogram using a mixture of normals (a priori distribution), in order to infer the a posteriori probability that a given pixel belongs to each component. With these probability values, we can classify the pixels (region segmentation), or even left some pixel unclassified, if the confidence interval is not wide enough (that is, there are two or more components with appreciable probabilty).
Due to the iterative nature of the EM algorithm, it is easy to use the current a priori model and the input data to update the parameters of the mixture. We obtain a flexible and efficient model to perform multilevel dynamic thresholding in the scene. Particularly, the technique has two important advantages: On the one side, due to its probabilistic nature, we can achieve very good results at a very low computational cost by simply sampling some random points over the image. This makes the process faster without significant qualitative impact in the solution. On the other side, as it is clearly adaptive to the input data, it achieves good results in presence of changing light conditions, with real time response. In addition, the technique can be easily extended to cope with color images, by simply augmenting the dimensionality of the input samples from one variable (gray level) to three (red, green, and blue values of each pixel).
Figures 2-a and 2-b illustrate bilevel thresholding (object-background) in the same image with different lighting conditions. Histograms appear superimposed on the respective segmented images, together with their mixture models.


Segment Finding and Tracking on Edge Images
The last application presented is related to medium-level visual perception. Based also on mixture models, and by using a slightly different probability density function as the basic component of the mixture, we developed an algorithm to find and track straight segments on edge images. The output of the algorithm can be used for a posterior high-level processing, e.g. 3-D interpretation.
The task of segment finding is considered as a parameter estimation problem. Segments are modeled by special probability density functions, and the edge image is considered as a random sample taken from a mixture of those elemental densities (see Figure 3-a). Again, the mixture parameters are estimated by a modified version of the EM algorithm: the probability that every point has been generated by a given segment is used as a weight to recalculate the extreme points of that segment in an iterative process. The solution quickly converges to a good explanation of the whole edge image in terms of straight segments. Moreover, given a sequence of image frames, the current solution is updated in a natural way, efficiently tracking changes in the scene, without restarting the iterative process. Finally, the model also contains a component to find isolated noise points, in order to cope with low quality edge images. Figure 3-b and 3-c show, respectively, a sample edge image and the obtained line model.
Conclusions
We show how simple techniques with the same underlying idea can be used in several fields of computer vision. In particular, we took advantage of the adaptive nature of the EM algorithm and of the conjugate properties of some density functions to perform on-line learning tasks at a low computational cost.
References