The Support Vector Machine (SVM) is an inductive learning method based on the Structural Risk Minimization principle (Vapnik 1995). It controls its own capacity, even when working in extremely high dimensional (implicit) feature spaces. This justifies the satisfactory generalization results demonstrated in many real world problems. However, using high degree kernels, SVMs can actually separate almost any distribution of examples, which is a potential drawback from the viewpoint of Vapnik?s Uniform Convergence Learning Theory.
The method of Random Falsifiability (RF) (Ruiz 1997) is a qualitative generalization predictor based also on the Uniform Convergence framework. It is appropriate for learning machines with controllable capacity that try to minimize the empirical error. The RF method has been successfully evaluated over standard learning algorithms such as linear discriminant functions, decision lists, multilayer perceptrons or decision trees. It is especially useful in adverse situations in which the problem distribution and the properties of the learning machine are unknown and additional test examples are not available. It can be considered as the simplest possible capacity control method. This work addresses the suitability of RF to predict generalization of inductive hypothesis generated by SVMs.
From Vapnik?s Uniform Convergence theory of Learning, it makes sense to accept a hypothesis with low empirical error Ê only if the maximum difference between the true error E and Ê is small for all possible hypotheses. This can be guaranteed in a probabilistic sense when the expressive power (capacity) of the learner is limited. Bounds on the rate uniform convergence in terms of the VC dimension of the learner are typically used.
Let Ê be the empirical error of the hypothesis h proposed by a learning machine M to explain a training set T of size n. Let T? be a modified training set obtained from the original T by changing the true label li of each example xi by a random label ri. Let R be the empirical error rate of the hypothesis h? obtained by M over the random training set T?. (Learning from both T and T? must be performed by the machine M using the same hypothesis class).
Random Falsifiability method. If Ê is large, reject h. If Ê is small, generate T? and obtain R. If R is also small, reject h. If R is large (close to the random prediction rate), accept h.
In other words, given an inductive hypothesis h with low empirical error, if random labels can be learned, h is not reliable (null average generalization) and should be rejected. If random labels cannot be learned, h is promising and can be accepted. In this case the training sample size n is large in relation to the expressive power of the learning machine, and therefore, the empirical error Ê will be close to the true error probability.
The RF method logically follows from the Uniform Convergence theory (Vapnik 1995) under reasonable assumptions. Here we present a brief outline of the derivation. The bound on E based on the annealed entropy can be rewritten in terms of a related magnitude, the probability of consistency C(n), showing that generalization requires exponential decreasing of C(n). This implies that the probability of incorporation ki of additional examples to a given hypothesis must be extremely close to ½. From this result, and using combinatorial arguments, it can be easily shown that the uniform convergence requirements for generalization implies large R, higher that 20%±5%. Lower values indicate that generalization will be obtained only by chance. On the other hand, it can be shown that the "rigidity" evidenced by a large R @ 50% suffices to meet the generalization requirements if the learning machine provides solutions that approximately minimize the empirical misclassification rate. Otherwise, Ê, and specially R, would be meaningless. Moreover, the capacity of the learning machine must be limited, avoiding situations where some kind of explicit memorization is combined with a fixed hypothesis class. The RF method uses the implicit exploration, in a single learning process, of alternative subsamples of a common training set.
Capacity control in SVMs is performed by selecting the optimal hyperplane in some (implicit, possibly high dimensional) feature space. Non linearly separable situations are typically solved by imposing a penalty to missclassified vectors, establishing a trade-off between margin width and (a bound on) the error rate. However, there is not an easy way to limit the capacity of a nonlinear SVM: convolution kernels such as radial basis functions or high order polinomials may accomplish perfect separation of any data set, just by using a sufficiently large number of support vectors. Almost all data sets become linearly separable in the feature space defined by those kernels, leading to infinite VC dimension. (Burges 1998). Furthermore, the SVM does not define a learning structure independent from the data, and hence, it is not a rigorous implementation of Structural Risk Minimization. From a simple "leave-one-out" argument, it is well known that E{P(error)} £ E{proportion of support vectors}, which is consistent with the intuitive relationship between expressive power and the number of support vectors actually used by the learner. Unfortunately, an expected value bound cannot be easily applied in practice; there are particular situations in which a decrease in the number of support vectors is not directly associated to better performance.
In these circumstances, a simple, qualitative validation procedure, such as the RF method, would be extremely useful. However, RF requires that the learning stages with both true labels and random labels is done with instances of the learning machine of the same capacity. Nonlinear SVMs with the previously mentioned kernels can always find a perfect solution, just by using a sufficiently high number of support vectors, increasing its capacity as required by the complexity of the data. The RF method cannot be directly applied to such kind of infinite capacity SVMs (both Ê and R will be always zero). Nevertheless, it is possible to design a similar randomization experiment to detect situations where the separation cannot be attributed to pure interpolation.
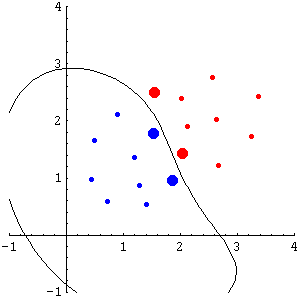
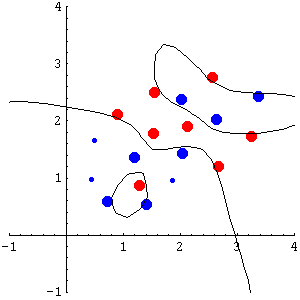
Random Falsifiability method for Nonlinear Support Vector Machines. If the proportion of support vectors S used by the solution h for the true class labels if similar to the proportion of support vectors T required to separate the examples with random labels, then h is not reliable and should be rejected. If S << T, h can be accepted.
The method directly follows from the principles of standard RF. If the proportion of support vectors is similar with both true and random labels, the capacity of the machine will be also similar, and hence the RF method can be safely invoked to reject the hypothesis h. Alternatively, due to the fact that the SVM always finds a global minimum, if the number of support vectors is much greater with random labels, it is clear that the error obtained with a lower proportion of support vectors would be necessarily higher than the one obtained with random labels. Therefore, RF can be invoked to accept h. Figure 1 illustrates the proposed validation method (using RBF kernel). In this simple example S << T, suggesting that the solution obtained by the SVM will show acceptable generalization.


Preliminary experiments with artificial data indicate that our method provides qualitative but still useful information on the validity of inductive hypothesis generated by SVMs. From the results of exhaustive experimentation on natural data we measure the accuracy of the method and characterize the kind of learning situations in which it can be safely applied.
References
Burges, C.J.C (1998). "A Tutorial on Support Vector Machines for Pattern Recognition". To appear in Data Mining and Knowledge Discovery.
Ruiz, A. (1997). "Practical Prediction of Generalization by the Method of Random Falsifiability". Tech. Rep. DIS-9-97, Department of Computer Science, University of Murcia. (submitted to Machine Learning).
Vapnik, V.N. (1995). The Nature of Statistical Learning Theory. Springer.