The Support Vector Method and the fdp estimation. In the last years, a powerful approach has been made on learning theory by Vapnik [1] with the Support Vector Machines, in different problems such as classification or regression [4,5,6]. The purpose of this communication is to examine today problems on probability density estimation using the Support Vector Machines (SVM).
A reasonable pfd estimation is a model combining a finite set of functions,
![]()
with its base functions guarantying an approximation to the true pdf by being themselves a pdf: parametric versions of a basic model, scaled and shifted, such as gaussians or derivatives of sigmoid functions.
The problem is to find an estimator for the pdf given the empirical data ![]() . Vapnik suggests the equivalent problem of solving
. Vapnik suggests the equivalent problem of solving
![]()
with ![]() the unknown probability distribution function of X given the data. Instead of the exact probability distribution function we can consider its empirical distribution function (EDF), constructed as
the unknown probability distribution function of X given the data. Instead of the exact probability distribution function we can consider its empirical distribution function (EDF), constructed as
![]()
where ![]() is the unity step function.
is the unity step function.
SVM for pdf estimation. Applying the concept of SVM, we construct a feature space, and a linear approximation to the pdf in it:
![]()
So, we can obtain
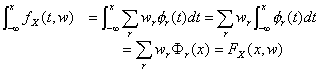
and both the density and the distribution space can be generated by the Mercer kernels,
![]()
The SVM regression function is found to be
![]()
where the activation kernel functions with preceding coefficients different from zero are the so called support vectors, and for the final solution the pdf is given by:
![]()
But in fact one of the conditions imposed to the SV coefficients [6] is ![]() , and this is not guarantied to be a pdf.
, and this is not guarantied to be a pdf.
Direct method approximation. One alternative view [3] is not to use SV regression, but directly minimize the actual risk of the described model, this is,
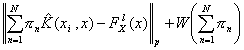
where the first term represents the empirical risk on a given norm and the second term is the structural risk imposing a regularization in the sense of Tikhonov.
Note that the width of the kernel is assumed to be the same for all of the activation functions; this is because the optimization task reduces to a quadratic programming problem. However, this is a lost of flexibility on the model, differing from the classification and regression problems support vector based.
One possible solution has recently been given by Weston et al. [2], proposing the use of a set of kernels ![]() having each one a different width
having each one a different width ![]() , with a linear computation increase for the required precision.
, with a linear computation increase for the required precision.
Limitations on the width. We propose two different approach which solve the fixed width parameter limitations. The first of them is to look for the width on each kernel on a continuous range with the same model. The second one is a different approach by transforming the minimization problem on a classification SV problem.
By using a continuous range on width parameter, the dependence of Mercer kernel on distribution function space will depend not only on the coefficients ![]() but also on each corresponding width
but also on each corresponding width ![]() . The problem, for a L2 optimization, is:
. The problem, for a L2 optimization, is:
Minimize:
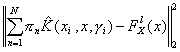
subject to:
![]()
![]()
![]()
This is not a general quadratic or linear optimization problem, but nevertheless can be done by using a classic method as generalized projected gradient [7], and its computational burden can be obtained comparable to quadratic programming by taking account of the nature of our specific problem. Limits on dynamic range for ![]() supposes a regularization on the generalization capability of the model
supposes a regularization on the generalization capability of the model
We introduce a new method for this estimation with SVM that changes the nature of the problem so it makes it insensitive to that value. Instead of attacking the problem of pdf estimation as a regression problem we turn it to a classification one.
Using the training set ![]() we obtain the
we obtain the ![]() as in the regression problem and with this function we construct two classes or hypothesis:
as in the regression problem and with this function we construct two classes or hypothesis:
![]()
![]()
At this very moment we have a classification problem that can be solve using Support Vector Machines. The resultant frontier will be the approximation to the distribution function and its derivative to the density one.
If we represent ![]() as
as ![]() and
and ![]() as
as ![]() we can obtain the distribution function,
we can obtain the distribution function, ![]() , as an implicit function:
, as an implicit function:
![]()
Where:
![]() are the values of the support vectors
are the values of the support vectors
![]() is 1 of H1 and –1 for H2
is 1 of H1 and –1 for H2
![]() is the kernel function
is the kernel function
If the kernel is of the RBF type the DPF is a explicit function of ![]() and
and ![]() :
:
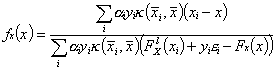
The![]() is not a sum of gaussian functions and its dependence with the width of the RBF is not strait forward. Moreover if we do not look it as a classification problem the kernel function helps us to change the input space to a higher dimensional one. In that higher dimensional space a hyperplanar decision boundary can be drawn and its projection into the input space will be the
is not a sum of gaussian functions and its dependence with the width of the RBF is not strait forward. Moreover if we do not look it as a classification problem the kernel function helps us to change the input space to a higher dimensional one. In that higher dimensional space a hyperplanar decision boundary can be drawn and its projection into the input space will be the ![]() estimate.
estimate.
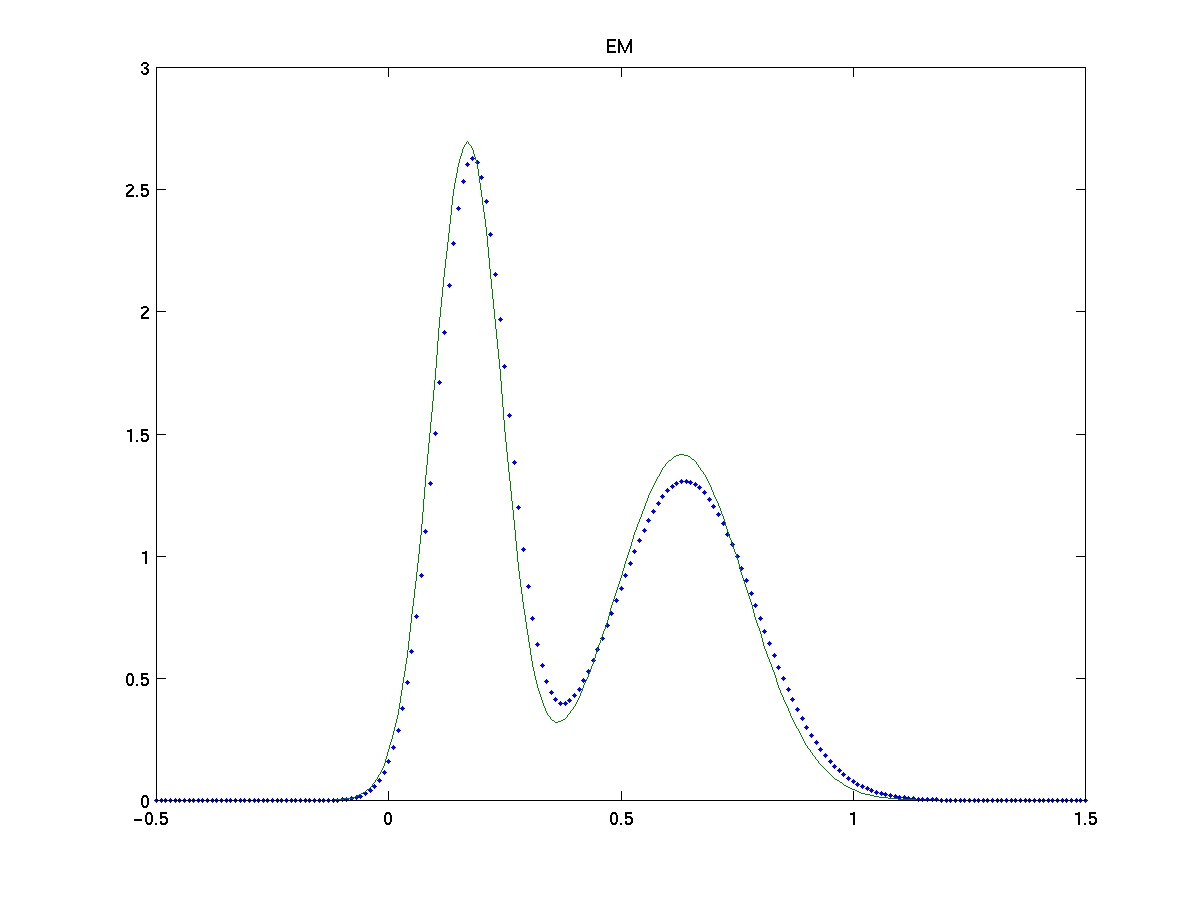
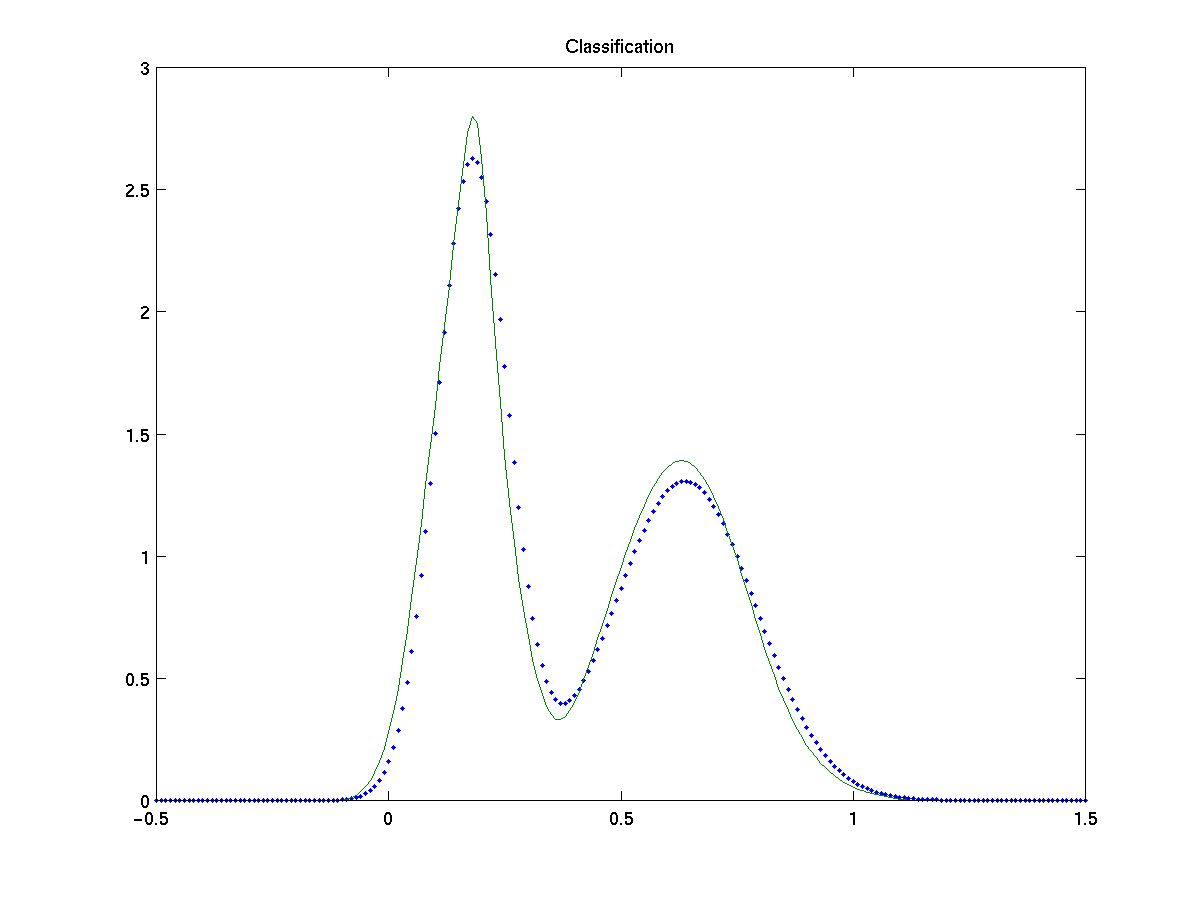
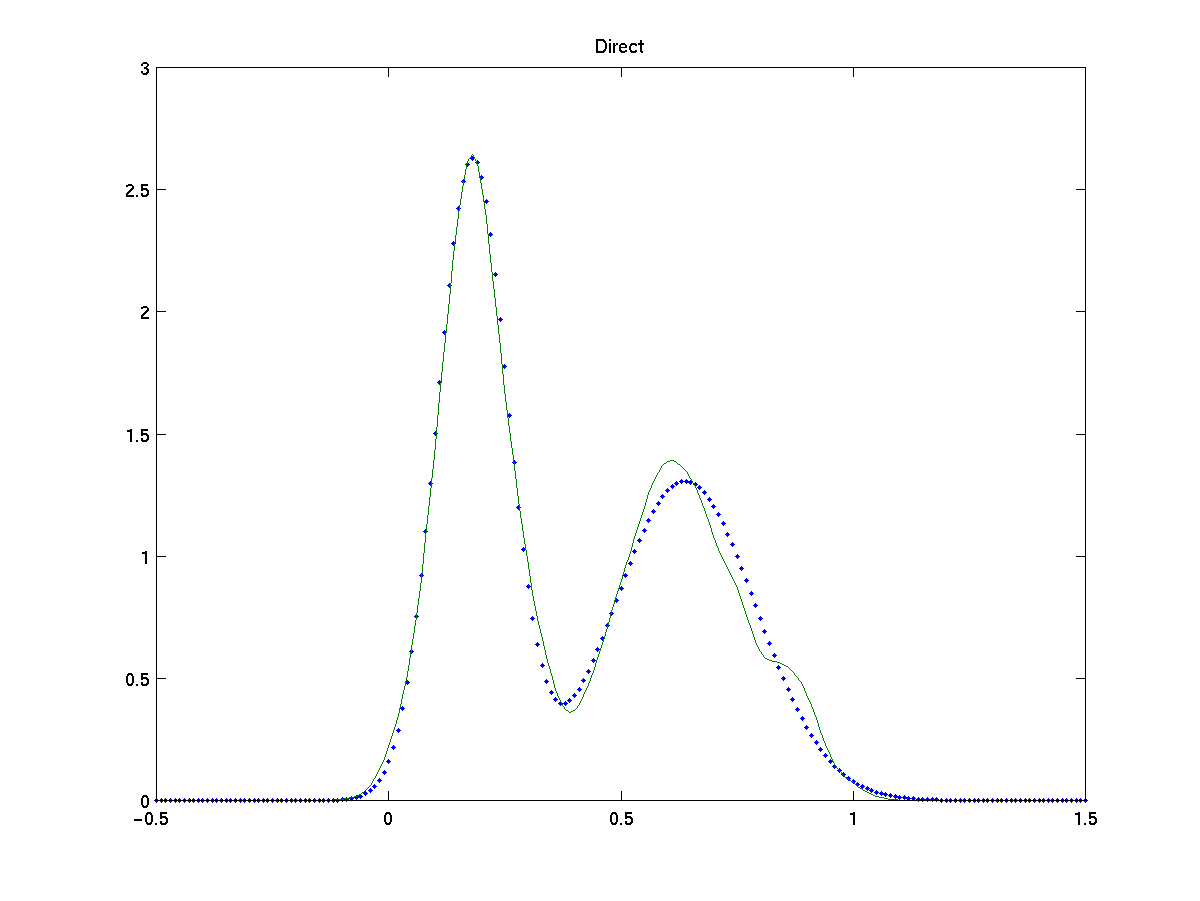
For a simple test on both methods we estimate the model for a mixture of two gaussians, N (0,0.5) and N (3,1), on 200 samples. We compare the results with the EM algorithm [9], a parametric method which maximizes the log-likelyhood from incomplete data assumed known the true number of gaussians.
Figures show the comparison of EM algorithm, classification based and direct width optimization with the true fdp (dots). Both approach give a high-quality approximation to the true pdf and equiparable to the one obtained by EM. Note also that proposed approaches are non parametric methods, as they make no assumption on the number of gaussians in the model, nor about the specific distribution of the data, which makes them more flexible.